KineBody Pro

Movable 3D Human Model






Help: Topics

(last updated 240611)

Additional details & instruction about KineBody are provided on this page.



Rotation Axes

The straight colored lines that appear in the KineBody Pro viewing area are rotation axes. They're colored red, blue, and green, for use with body rotations, or, magenta, yellow, and/or cyan, for moving a joint.


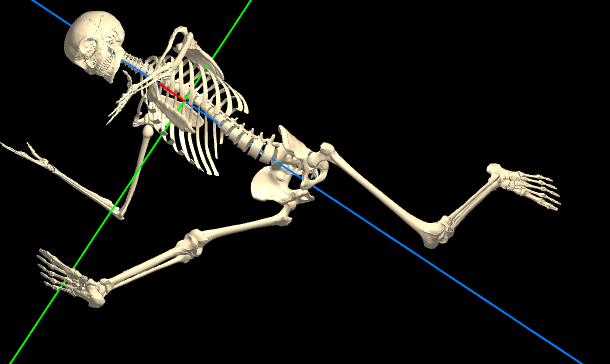
Axes for body rotations: Red, blue, green
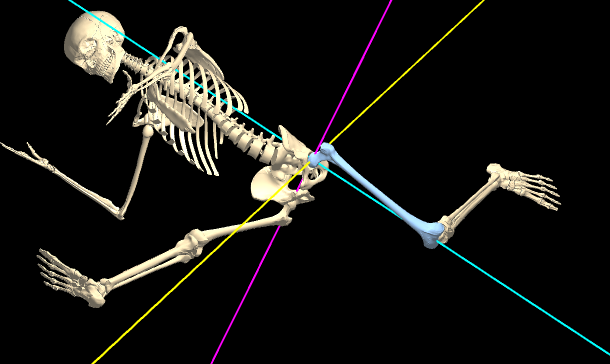
Axes for joints: Magenta, yellow, cyan

Troubleshooting: If the colored axes aren't visible, there may be a couple of reasons: a) the Show Axes checkbox in the Show subpanel is turned off, b) the relevant body part(s) and rotation center are displaced off the screen, either by an excessive value of horizontal or vertical position, or, when the distance is very close. Any/all of these issues can be alleviated just by pressing the Fit button (lower left).
Another potential issue: you can see blue and green body axes, but not red. The red axis always points normal (perpendicular) to the screen, and when it's centered in the viewing area, its projection onto the screen may be small. If you displace the body position away from the viewing area center, KineBody Pro's simulated 3D perspective causes the projection to become more visible.
Finally: only a single set of 1 to 3 axes is shown at at time, to minimize clutter. The visible axes are the ones associated with the current joystick mode.

The axes play several roles in KineBody Pro:

The various rotation axes used in KineBody Pro exhibit highly consistent behavior and appearance, to simplify movement operations for a large number of joints, as well as for the body. The rest of this section intends to elucidate some of the properties and patterns associated with these axes.

One slider per rotation axis: Each rotation axis generally corresponds to one rotational degree of freedom (DOF), or equivalently, to one of the currently visible rotation sliders. When you adjust a rotation slider, you can observe a body part pivoting about one of these lines. For instance, when you rotate the full body, it should be relatively clear that the ‘tilt’ angle is associated with rotations about the green axis, and the ‘spin’ angle measures rotation about the blue axis.

The association between axes and sliders is indicated by the colored rectangle, at the right or top end of the slider (spin ≡ blue, tilt ≡ green). (Sliders that don't have a colored bar are for translational movement (horizontal, vertical, distance), not rotation).

Some rotation axes change direction, others remain fixed: As you experiment with various rotations, you may note that, not only does the body or joint rotate, but some of the axes change direction as well. Yet, other axes remain fixed, no matter what rotations you apply. For example, when you tilt the body, the blue axis changes direction, but adjusting spin or tilt doesn’t change the green axis direction. You can see a similar effect if you adjust the hip joint: of the three axes, the magenta one remains fixed to the hip bone, but the yellow and cyan axes may change direction, depending on the adduction/abduction and internal/external rotation angles.

There's a clear pattern for how the axes do or don't change direction. It's easiest to understand this pattern for the body axes (red, blue, green):

Note that the red and blue axes, although they 'start out' perpendicular, they don't have to remain so. In fact, they may coincide, when the tilt angle is + or -90 degrees (i.e., both pointing normal to the screen). This can lead to some confusion, because a body rotation about those coincident axes can be regarded as either dial or spin, or some combination of the two.

The way that the rotation axes move or not can be understood in terms of a sequence or hierarchy, in the order Red > Green > Blue (RGB). Under this hierarchy, if you pick one axis and rotate about it, the directions of the axes lower in the hierarchy may change direction, i.e:

For joint rotation axes, a similar pattern applies: the 'reference object' is the proximal bone, and the 'hierarchy' applies to the axes in the order = magenta, yellow, cyan (MYC). So, for 3DOF joints (such as the main (gleno-humeral) shoulder joint, or the hip joint (ilio-femoral)), the pattern is as follows:

For 2dof joints, there is one axis that remains fixed (to the proximal bone), and one that changes direction. For such joints, the 'MYC' pattern for 3DOF joints gets modified slightly:

For 1DOF joints, the (sole) rotation axis may be magenta or cyan; the choice of color generally follows logic similar to that for 2DOF joints:

As brief summary, the logic behind the axis colors for joints can be distilled into a prioritized list of conditions, as follows:

Exceptions: The MYC pattern just described holds for most joints, but there are several exceptions:

Euler angles: The body and joint rotation axes don't remain mutually orthogonal (perpendicular), so they can't be used as a Cartesian coordinate system. However, they can be used to define a set of a Euler angles (pronounced 'oiler')(a.k.a, Tait-Bryan or Cardan angles), which can serve as a 'coordinate system' for spatial orientation. In KineBody Pro, an Euler angle system is used for characterizing the rotational position of the body and all joints, thereby making it possible to define their positions precisely as well as practically.

Most presentations about Euler angles include a good dose of math, involving trigonometry and matrix multiplication. For the current discussion, it's not necessary to understand the math behind Euler angles; but it may help to understand some of the qualitative aspects, i.e., the 3D geometry regarding which axes move, as presented above. (On the other hand, if you have some background in Euler angles, the patterns described here should be relatively easy to understand).

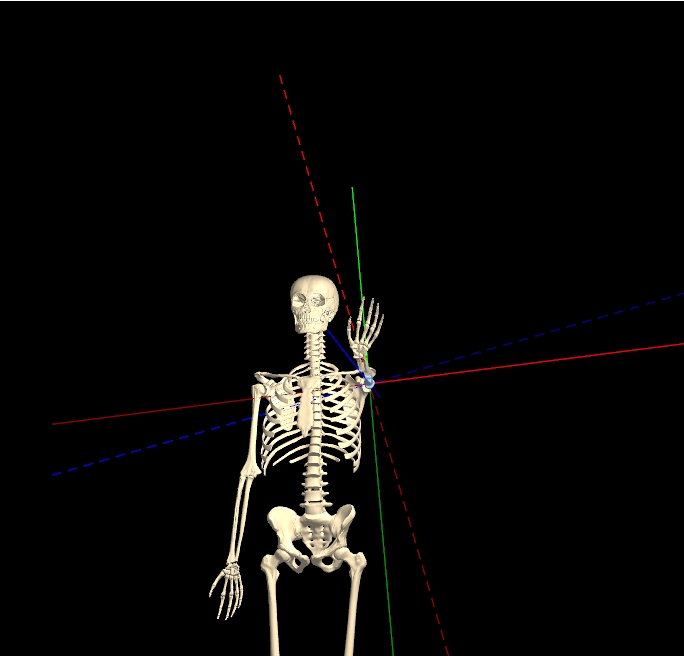
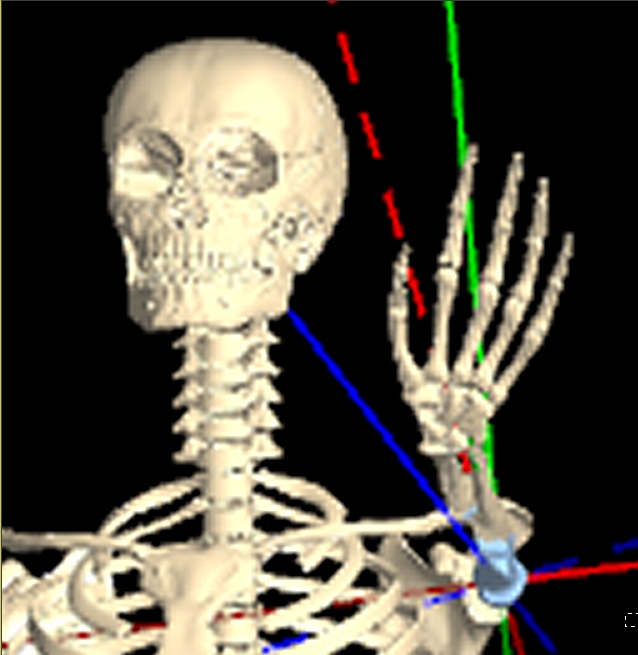
Other axes: For body rotations, the spin,tilt, and dial angles form an Euler angle system, but there are some special 'non-Euler' body rotation angles available for adjustment, labeled rot horz and rot vert in the KineBody Pro app. Some of the special properties for these rotation axes include:

Summary: The rotation axes in KineBody Pro aren't arbitrary: rather, they exhibit consistent patterns of properties and behaviors. Operation of the KineBody joystick is strongly connected to this pattern, so that you can easily move (almost) any joint in the same manner as any other joint.


Degrees of Freedom

In a loose sense, a ‘degree of freedom’ (DOF) refers to one of the ‘directions’ you can move a joint. For example, the glenohumeral joint of your shoulder has three primary degrees of freedom:

In contrast, the humero-ulnar joint of your elbow has one primary degree of freedom (flexion & extension). It’s important to understand, however, that ‘degrees of freedom’ are not the same as ‘directions’. Differences include:

  1. ‘Directions’ is a very vague term. For example, you can move your arm to the left, or you can lift your knee upward, but the effect of these motions on your joints depends on how your body is oriented. For human joint motions, it’s helpful to describe the motions in relative terms, i.e., how one body part moves relative to another. Thus, you can move your arm away from your body (abduction), or you can move your knee in a sagittal plane (flexion/extension) so as to change the angle between femur and tibia, etc. For a joint, degrees of freedom generally refers to relative motion, between the adjacent bones.

  2. A ‘direction’ can refer to:
    1. either of two possible motions along a line (for instance, up or down), or
    2. both of these together (vertical).
    A ‘degree of freedom’ generally refers to the latter: ‘both together’. Thus, the combination of flexion and extension constitutes two directions but only ONE degree of freedom.

It’s also important to understand that degrees of freedom do not refer to the measurement of an angle in degrees! [For instance, don't ever refer to a 30° range of motion as ’30 degrees of freedom’! Although the words are logically correct, they're not 'idiomatically' correct. ]

More specifically, ‘degrees of freedom’ refer to the independent coordinates required to completely specify a position or direction. For example, if you’re using a touch screen, the position of your fingertip as it slides along the screen has two degrees of freedom, which can be specified using Cartesian (x, y) coordinates relative to the screen edges. Note how this differs from ‘directions’: you can move your finger an infinite number of directions, or, to an infinite number of positions.

Generally, a point in physical space is considered to have 3 degrees of freedom, corresponding to the Cartesian (x,y,z) coordinates required to specify its position. It’s not essential to use Cartesian coordinates: you could alternatively express the position using cylindrical (r, θ, z) or spherical (ρ, θ, φ) coordinates. Regardless of the type of coordinates, the number of degrees of freedom remains the same. For a rigid body in space, there are 6 degrees of freedom: 3 to specify the position of one point on the body, and 3 to specify the orientation of the body relative to that point. The orientation is often expressed as 3 rotations: for instance, the orientation of a flying aircraft is often specified in terms of the the yaw, pitch, and roll angles, relative to the earth.

The number of degrees of freedom is reduced whenever motion constraints are present. If you consider your fingertip to be a ‘point’, it has 3 degrees of freedom in general, but only 2DOF while it remains in contact with a touch screen. The touch screen contact is a 1 DOF constraint, i.e., you’re prevented from moving your finger into the screen.

It’s useful to consider a similar case, of moving your fingertip over the surface of a curved object, for example, a ball. In this case, there is once again a 1 DOF constraint, preventing you from moving your fingertip into the ball; thus, the position of your fingertip on the ball surface has two degrees of freedom – this is so even though the ball surface is three dimensional. This makes sense if you consider the analogous case of specifying your global position on the earth’s surface: only latitude and longitude are needed (unless you’re flying, scuba diving, etc).

KineBody represents the position of the full skeleton using 5 or 6 degrees of freedom, depending on which version of KineBody you’re using:

The 5 DOF case is simple to use and understand, and is adequate for most purposes, whereas the 6th degree of freedom introduces more complexity. Note that the reference for full body motion is the thorax, i.e., the rotation values are defined relative the ‘home’ position of the thorax, without regard to the positions of any other joints. Likewise, full body translations are defined to be those of the thorax (measured relative to an origin at your eye).

Joints in KineBody are represented using 1 to 3 DOF – the number and direction depends on the joint. As with the full skeleton, there is one slider control for each degree of freedom. All of the joint DOF’s are rotational – KineBody doesn’t currently implement translational DOFs for joints (despite their importance, for instance, at the tempero-mandibular joint). Hence, a 3 DOF joint (such as the gleno-humeral joint at the shoulder) permits 3 types of rotation. Note that the number of DOFs at a joint is defined by the relative motion between the adjacent bones – this doesn’t change whether you consider both bones to be free in space or for one of them to be fixed.

It may be useful to understand the number of DOFs at a joint in terms of the constraints: For instance, a 3 DOF ball & socket joint can be understood as follows:

total DOF for two independent bones in space 12 (2 bones x 6 DOF per bone)
debit for considering only relative motion -6 constraint DOFs
debit for ball & socket joint -3 constraint DOFs (ie, 3 translations are prevented)
Net 3 actual DOFs

KineBody currently implements more than 75 DOF in total among all joints (of which over 60 are 'unique', when you discount left/right symmetry). Unfortunately, it doesn’t currently allow all possible human joint motions. Joints within the hands and feet are a priority, but aren't yet available simply due to the significant effort required, to implement more than 40 additional (unique) DOFs. Apart from these, the DOF available in KineBody have been selected & prioritized using multiple criteria, to focus on the following

For some joints, different DOF can be defined, corresponding to different coordinate conventions. For example, the acromio-clavicular joint can be configured to define DOFs relative to the cardinal planes [1], but research literature sometimes uses motions relative to alternative axes, along the plane and spine of the scapula [2]. KineBody follows the latter convention, allowing the measured & published ranges of motion to be used directly, i.e., without requiring additional coordinate transformations.

An important notion related to degrees of freedom is the concept of euler ‘sequences’, i.e., the order in which the rotational degrees of freedom are applied, when a body is rotated to a position ‘between’ (or, in a combination of) the independent degrees of freedom. For more info, stay tuned for a future writeup on Euler angles.

References

  1. Neumann, Kinesiology of the Musculoskeletal System, 2nd Ed (ch 5).
  2. Ludewig, et al., 'Three-dimensional Scapular Orientation and Muscle Activity at Selected Positions of Humeral Elevation', Journal of Orthopaedic & Sports Physical Therapy, 24:2, Aug 1996.

FFI



Distance vs. Zoom

In KineBody, a Distance slider is provided to make the objects appear larger or smaller, instead of a conventional Zoom slider. This approach makes it possible to use physically meaningful position measurements. For example, if the distance slider’s numeric readout says 5.0 (meters), KineBody appears the same size as a physical human (full grown, ≈1.8m tall) at that same distance. This isn't possible using a Zoom scale – zoom is normally defined as a simple, unitless multiplier, e.g. ‘2x’, to represent the case where an image has been enlarged to twice its original size. The problem arises because the ‘original size’ can be any value – it doesn’t have to have any connection with physical distance.

A more subtle difference between distance and zoom is caused by viewing a perspective in 3D: if you consider two objects in the same view, one near, one far, the proportion of their size changes with distance, when you view them in 3D. A zoom control, on the other hand, usually only enlarges the objects, keeping the size proportions the same. The following figures demonstrate this idea: the Figure 1 is for reference, Figure 2 shows the effect of enlarging a 2D copy of Figure 1, as is done with most Zoom controls; Figure 3 shows the effect of changing distance, using KineBody. As you can see, the skulls are effectively the same size, but the hand is significantly larger in Figure 3, owing to the use of proper 3D perspective.

KineBody at original position
Figure 1. Original View
KineBody at 5x zoom
Figure 2. 5x Zoom (2d enlargement)
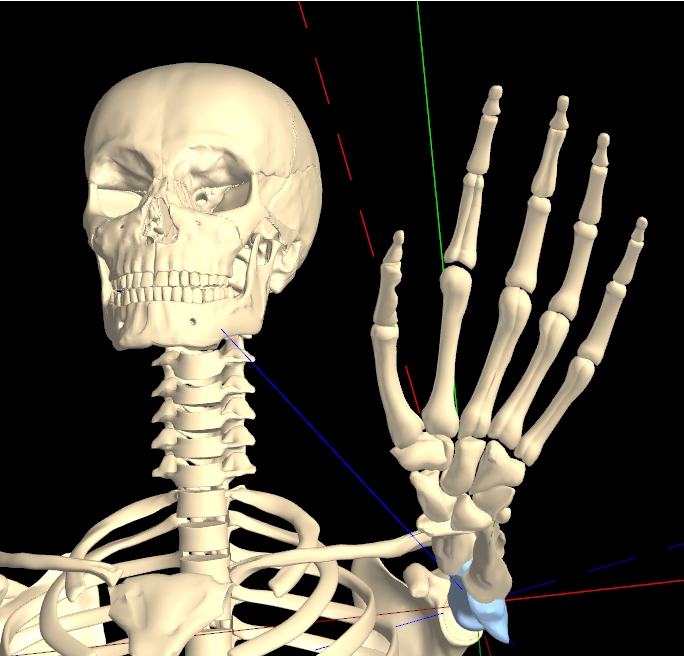
KineBody at 20% distance
Figure 3. 20% distance (3D perspective)

From these figures, it should be clear that the Distance control in KineBody doesn’t behave the same as a conventional Zoom control. Hence, the alternative terminology.

As you might have surmised, there are some assumptions required to make this work. The size of your monitor, as well as its distance from your eyes, are two key parameters required to express KineBody’s size in terms of distance. The distance calibration in KineBody currently assumes a screen 0.2m high, positioned about 0.7m from the eyes. If your monitor size or eye-to-screen distance differs, the distance calibration in KineBody may be inaccurate. However, what actually matters is the ratio of these parameters: 2/7, or ~ 0.29. If your monitor size is 0.3m, but your eye-to-screen distance is about 1.0m , the calibration will be close. Ultimately, however, the calibration depends on KineBody’s physical size. That is, if your monitor is large and close to your eyes, KineBody will appear larger or closer than its nominal 1.8m height would suggest. So, accurate calibration isn't essential. (On the other hand, if you desire precise calibration, a custom distance calibration widget is planned for a future edition of KineBody).

[Note; the distance calibration may be incorrect, if you're using Windows and Firefox. Windows allows you to increase the size of text & other items, e.g., to 125% of its normal value. This Windows setting is used within Firefox to change the size of graphics elements, with the result that the distance calibration may be incorrect. You can correct the calibration by using the Firefox's zoom control (main menu>View>Zoom). For example, if your Windows text size is 125%, set the Firefox zoom to 80%: Under the Zoom menu, press Reset & then Zoom Out, then Zoom Out again. (to change from 100% to 90% to 80%). Of course, this all presumes that your screen size & distance follow the 0.29 ratio above. Any other value will cause additional discrepancies].

A related parameter is the location of the ‘zero’ distance point, which may become relevant when you’re examining KineBody at close distance. KineBody currently defines zero distance at point in the middle of the ribcage, as shown by the intersection of the red, blue, and green axes when full skeleton movement is enabled. [This point is more or less arbitrary: it actually represents the geometrical centroid of all the spatial points used to define the the ribcage; note that this is not the same as the center of gravity, of either the ribcage or the full skeleton].



Bone & Joint Hierarchy


The KineBody skeleton contains over 200 bones, some of which are connected rigidly to each other, forming 'units': the skull, thorax, hands, feet, and mandible [5]. Following is an organized list of the bones and joints, showing their relation to each other. Contents of the bone units are listed thereafter.

Every joint has an associated distal bone, so these are listed as together, e.g. ‘sternoclavicular joint / clavicle’. Indentation of text indicates a serial connection, e.g., the acromio-clavicular joint (indented relative to the previous line) connects the clavicle to the scapula. Joints sharing the same indentation share the same parent bone or unit. 'L/R' indicates that the bone or joint appears as either Left or Right; this designation is inherited by all bones or joints lower in the hierarchy.


Footnotes
[1] The Occiput-C1 joint cannot be independently moved - it can only be moved as part of the neck (joint) group.
[2] 'Mandible' is used as the name of a bone unit, and as a bone within that unit, i.e., the mandible unit includes the mandible bone + lower teeth as well.
[3] The L5S1 joint cannot be independently moved - it can only be moved as part of the lumbar spine (joint) group.
[4] The coccyx was omitted in the original ('KineMan') version.
[5] The terminology was changed from 'bone group' to 'bone unit', as of March 2021, to avoid confusion with other types of groups (i.e., groups of bones used for copy/paste and show/hide selection, and joint groups).


[Note that this hierarchy defines the organization of linkages specifically for use by KineBody; it doesn’t necessarily reflect the groupings normally used for kinesiological or biomechanics study. For example, for KineBody operation, the humero-radial joint is absent, and the proximal & distal radioulnar joints are combined into a single entity].


Bone unit contents:

Unit Contents
Skull (L/R, 2 each): parietal, temporal, ethmoid (orbital & cribriform plates***), maxilla, palatine, zygomatic, lacrimal, teeth (upper); 3 nasal conchae
(non-L/R: 1 each): occiput, frontal****, sphenoid, nasal, crista galli, vomer, ethmoid (perpendicular plate etal***)
Thorax 24 ribs, 12 T vertebrae, 1 sternum
Proximal carpus 1 each: lunate, scaphoid, triquetrum, pisiform
Central pillar (of hand) 1 each: hamate, capitate, trapezium, trapezoid; metacarpals 2 & 3
Metatarsal 1 1 metatarsal, 2 sesamoid;
Midfoot 1 each: navicular, cuboid; 3 cuneiform; 4 metatarsal
Mandible 1 mandible (bone), 2 teeth lower (L/R)

*** The ethmoid bone in this set is split into distinct parts, including the orbital and cribriform plates, plus 'perp' ( perpendicular plate) and 'repg' (lamina perpendicularis pars repugnante).
**** A portion of the frontal bone is this set shows as 'sinf' (for 'sinus frontalis').



Body Options

KineBody Pro provides users with a choice of 3 bodies: two ‘median’ adult skeletons: male & female, plus a second adult male dubbed ‘original’ or ‘KineMan’, which was the sole skeleton offered in prior versions of this software (2013-2020). This section provides some background regarding these options. Related information is available at the instructions page for body selection.

Bones for all three of these skeletons were obtained (or derived) from a commercially available bone dataset [1]. This bone dataset includes male & female bones; the female bones are typically just scaled replicas of the male bones, i.e., the shapes are identical. The pelvic bones are an exception: they’re shaped differently for male vs female, to represent the natural differences in those bones.

The KineMan original skeleton was assembled from the male bone data “as is”, for the most part, i.e., generally without modification in size or shape. Bone positions were fine-tuned for improved joint accuracy and initial posture.

The original skeleton was adequate for it’s primary original design goal, which was to accurately depict 3D human joint behavior, for all high-mobility joints. A secondary design goal was to serve as a simple human pose demonstration tool, for use in applications such as athletics/martial arts/ dance, visual & performing arts, and similar. For many of these purposes, the overall height of KineBody skeletons is irrelevant: you can visually “scale” the body size simply by adjusting the body distance. Similarly, the sizes and proportions of bones is often irrelevant. For instance, the bone sizes are unimportant if your goal is to demonstrate/observe joint mechanics.

One motivation for developing new body types arose while investigating the validity of the scale and proportions of the original dataset. Upon comparing the dimensions of the original/KineMan male skeleton and an ‘average’ male, several discrepancies became apparent. The height of this skeleton is 1.85m (6’1”), whereas the average for U.S. adult male height is closer to 1.75m (5’9”), and not significantly taller for other parts of the world [2]. Furthermore, the proportions of the head and neck appear to be relatively small & large (respectively): the ‘original’ head height is approximately 0.105 of body height, whereas many sources suggest that typical human heads are larger, in the range of 0.12-0.133 of height [3]. The tibias of the original data set also appear to be unusually long.

The two median skeletons were derived from the original KineMan skeleton, by rescaling the individual bones so as to closely align with median (i.e. 50th percentile) body surface measurements, obtained from a population of over 6000 American male and female individuals [4]. The body surface measurements weren’t always sufficient for this task, so the measurements were supplemented with skeletal proportions from CT scans of an individual adult male [5], and corroborated with images of average body shapes [6]. The female median skeleton was constructed likewise, but using the special female pelvis bones provided with the original data set.

Many of the differences in proportions between the original and median male skeletons are evident from a cursory view: the median body has a larger head, shorter neck, and shorter tibias, as shown in the Figure below. Some other differences are subtle: the median body has a narrower ribcage, wider shoulders and a flatter clavicle inclination, larger hands and longer humerii.

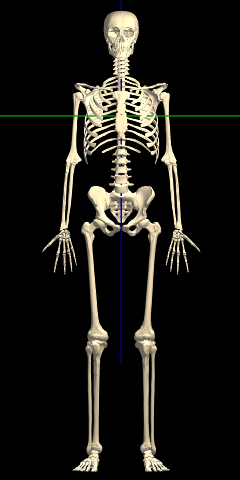
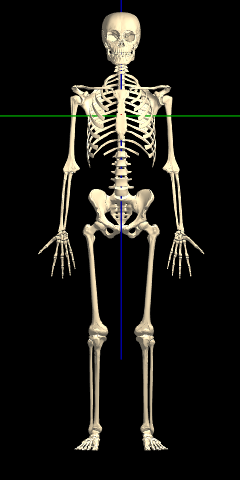
Original (left) vs Median (right) Male Skeletons

Between the male & female median skeletons, the only immediately obvious difference is in the hips. All the other differences are very subtle: when you change between the median male & female bodies, it appears that the female is simply a smaller (or farther) version of the male:

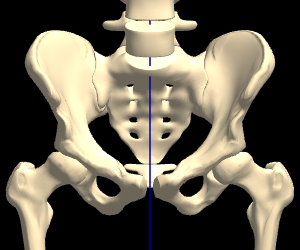
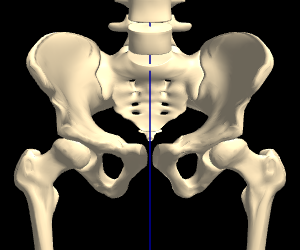
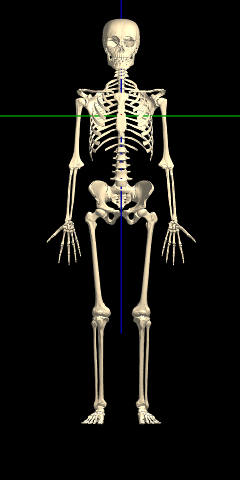
Median Male (left) vs Female (right) Pelves
Median Male (left) vs Female (right) Skeletons

However, when the female is scaled to the same height as the male (via a distance change), and overlaid, the differences in proportions become more evident (hover the image, to alternate between Male & Female):

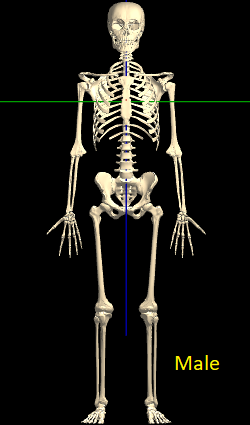
Median Male vs Female Skeletons (scaled to same height)
[ Hover to alternate image ]


[1] Anatomium.com (P1 dataset)
[2] ourworldindata.org/human-height
[3] Human Proportions for Figure Drawing,
     or Proko.com, Human Figure Proportions
[4] The 2012 Anthropometric Survey of US Army Personnel
[5] Visible Human Project
[6] By Nikolay Lamm, as reported in The Atlantic, This is the Average Man's Body